https://velog.io/@yerimii11/WEEK03-DAY20 2021년 11월 21일에 작성된 게시글 아카이브입니다. (사유: 블로그이전)
[WEEK03] DAY20 & TMI
크루스칼 알고리즘유니온 파인드 (합집합 찾기) (disjoint set 자료구조 : 서로소 집합)코드를 외우자 최소 3번 쓰기코드복습1 - 인프런 탐색, BFS DFS(일욜)보기 - 코드복습 213, 14 하 풀고 -> 7~12 중 풀고
velog.io
- 크루스칼 알고리즘
- 유니온 파인드 (합집합 찾기) (disjoint set 자료구조 : 서로소 집합)
- 코드를 외우자 최소 3번 쓰기
- 코드복습1 - 인프런 탐색, BFS DFS(일욜)보기 - 코드복습 2
[팀플]
7~10 중 풀고 -> 13, 14 하 풀기 (19 동전문제도 보기) <월요일 2시>
<화~> 위상정렬 -> 상 문제 순으로
- 깃 메인에 파일 잘못 올렸을 때
git pull main
풀 받고 실제 폴더에서 삭제한 다음
git add .
git commit -m "rm" 똑같이 하고
git push origin main 하면 끝
오늘 푼 문제들은 코드구현이 익숙치 않아서 팀원들과 함께 코드리뷰하며 많이 배웠다!! 코드를 최소 2번 더 복습할 예정.
그래프 탐색 기본
1197 최소 스패닝 트리


ㄴ 코드 (주석O)
# import sys
# v, e = map(int, sys.stdin.readline().split())
# a, b, c = list(map(int, sys.stdin.readline().split()))
# 크루스칼 알고리즘
# 유니온 파인드 (합집합 찾기)
from sys import stdin
input = stdin.readline
# V:노드의 갯수, E:간선의 갯수
V, E = map(int, input().split())
graph = [list(map(int, input().split())) for _ in range(E)]
graph.sort(key=lambda x: x[2]) # 가중치값을 기준으로 (배열)정렬해준다(유니온파인드 핵심)
ans = 0 # 우리가 찾으려는 가중치의 최솟값. 초기값 세팅
parent = [i for i in range(V+1)] # 부모노드 임의로 01234식으로 배열을 주고 찾음 0부터 v까지
# ㄴ여기 왜 i지?? -> i를 v번 반복해서 써줌 => [0, 1, 2, 3]
def find(a): # 원래 부모노드값 초기값은 위에 ┌ 배열 [0, 1, 2, 3] 니까.
if a != parent[a]: # 1이 들어오면 1의 부모값과 비교하고 둘이 같지 않으면 뭔가 경로가 바꼈다는 뜻.
parent[a] = find(parent[a]) # 같지않으면 부모 노드의 바뀐 값을 넣어서 한 번 더 찾아줌 (부모값바꿈)
return parent[a] # 그게 아니면 일반적인 자기 부모 값을 반환한다
def union(a, b): # 1번노드와 2번노드의 부모값이 들어옴
a,b = find(a),find(b) # 1번노드와 2번노드의 부모값을 찾음
# 2번노드의 부모값과 1번노드의 부모값을 바꿔버림. 둘이 이어졌다하면 루트노드를 바꿔야 이어졌다고 보니까
for i in graph:
a, b, c = i # 부모노드값이 같은지 확인하는거임. 그래서 다르면 연결시킴(union)
if find(a) != find(b): # 싸이클인지 아닌지 확인하는 구문 # 1번 2번 꺼내서 비교해보고..
union(a,b) # 둘이 같지않으면 떨어져있다고 가정하고 합쳐버림 (부모노드 연결)
ans +=c #가중치 합함 # 0번은 맞춰주려 넣은거니 무시해도 됨
#만약 a b c 값을 받았는데 노드 둘을 이었을 때 사이클이 된다면 스킵해버림(else) (최소신장트리는 사이클이 없어야해서)
print(ans)
# 7:25 // 25line 설명 // 2번노드의 부모값과 1번노드의 부모값을 바꿔버림. 둘이 이어졌다하면 루트노드를 바꿔야 이어졌다고 보니까
# union -> 1번 2번 꺼냄 비교. 경로는 모르지만 가중치는 아니까 1번노드의 부모값을 찾음
# 0번은 맞춰주려고 넣으니 무시, 그럼 find(a)는 find(1)이고, find(b)는 find(2)
# 20번째줄로 가서 a는 1, 부모노드의 1번 인덱스도 1 ([0,1,2,3,4])이니까 부모노드값 리턴 (1 리턴)
# find(b)도 2 넣었을 때 그대로 부모노드값 리턴2 (26line복귀)(리턴값이 나오면 둘이 이어져있지 않다는 것)
# 만약 20번째줄에서 둘이 같지 않으면 둘이 이어 (25->29line으로 내려감)> union 사용 >가중치 합지나가던 할머니도 이해하게 만들 아주 자세한 주석
ㅋㅋㅋㅋㅋㅋㅋㅋ
ㄴ 코드 (주석X)
# 1197 - 주석 없는 ver.
import sys
input = sys.stdin.readline
v, e = map(int, input().split())
graph = [list(map(int, input().split())) for _ in range(e)]
graph.sort(key=lambda x: x[2])
ans = 0
parent = [i for i in range(v+1)]
def find(a):
if a != parent[a]:
parent[a] = find(parent[a])
return parent[a]
def union(a, b):
a,b = find(a), find(b)
for i in graph:
a, b, c = i
if find(a) != find(b):
union(a,b)
ans += c
print(ans).
.
1260 DFS와 BFS
DFS는 재귀를 사용하고,
BSF는 큐,덱에 저장 후 반복문을 돌며 찾는 방식을 사용한다.
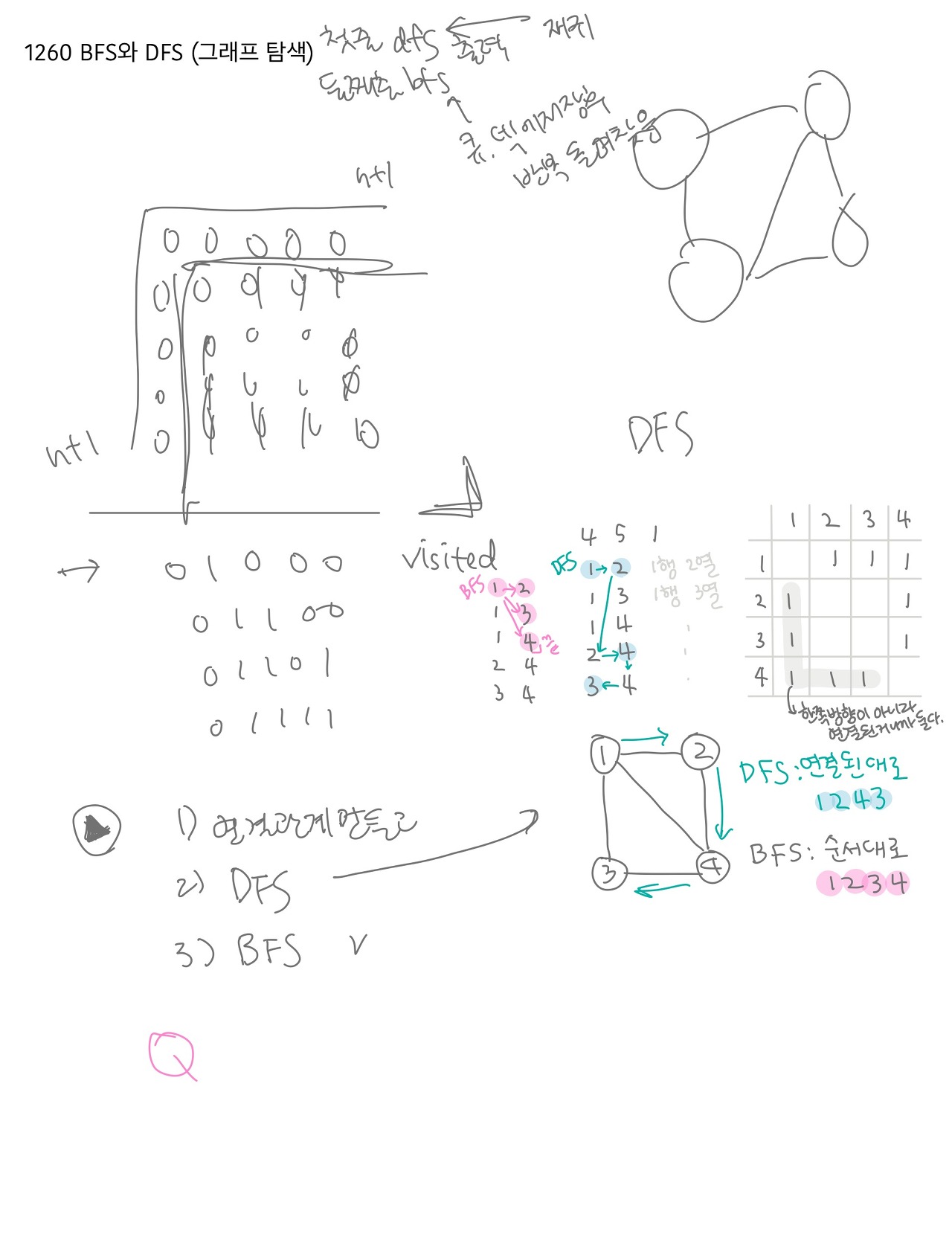
왼쪽윗부분은 팀원1의 풀이 방식(그래프)이었고,
나머지는 내가 문제를 해석하느라 쓴 메모들..! 오른쪽에 표 같은건 인접행렬
처음에 입력값과 출력값을 보면서
그래서 이걸 어떻게 구현해내야 하는거지..? 하는 생각을 한참했다..
이 문제가 앞으로 DFS와 BFS 문제를 풀어나가는 것에 대한 이해도를 높여주는데 도움이 된 문제였던 것 같다
ㄴ 코드
import sys
input = sys.stdin.readline
# 정점 갯수, 간선 갯수, 탐색 시작할 정점 번호
Vn, En, v = map(int, input().split())
V = {} # {}: 딕셔너리. 간선이 연결하는 두 정점의 번호가 들어옴(입력값 V[v1], V[v2])
for i in range(1, Vn + 1) :
V[i] = [] # 빈 리스트 채워줌 {1: [], 2: [], ...}
for i in range(En) :
v1, v2 = map(int, input().split())
V[v1].append(v2)
V[v2].append(v1)
for i in range(1, Vn + 1) :
V[i].sort()
gone = []
def DFS(now) :
print(now, end = ' ') # 가장 먼저 자기를 출력
gone.append(now) # 그리고나서 자기가 갔던 곳에 넣음
for i in V[now] : # 나우를 갈 수 있는 i에 대해서 i가 아직 안 간 곳이라면 DFS를 실행
if not i in gone :
DFS(i) # 1에서 실행하면 1이 출력되고, 2에서 DFS가 시작돼서 2가 출력되고 4에 대해 DFS가 출력되고 끝남.
DFS(v) # 그리고 1에서 3도 갈 수 있으니 3에 대해 DFS가 출력됨.
print()
gone = [] # BFS가 실행될 때 gone을 다시 비워줌.
def BFS(now) :
que = [now] # 큐를 만들고 큐에 나우 하나만 넣음
while que : # 큐라는 리스트에 아직 안 간 곳이 추가 됨
q = que[0]
print(q, end = ' ')
gone.append(q)
del que[0]
for i in V[q] : # V: {1: [2,3,4], 2: [1,4], 3:[1,4], 4:[1,2,3]}
if not i in gone and not i in que : # 이미 간 곳도 아니고 갈 예정도 아닐 때
que.append(i) # que:[] -> que: [2,3,4]
BFS(v).
.
11724 연결 요소의 개수
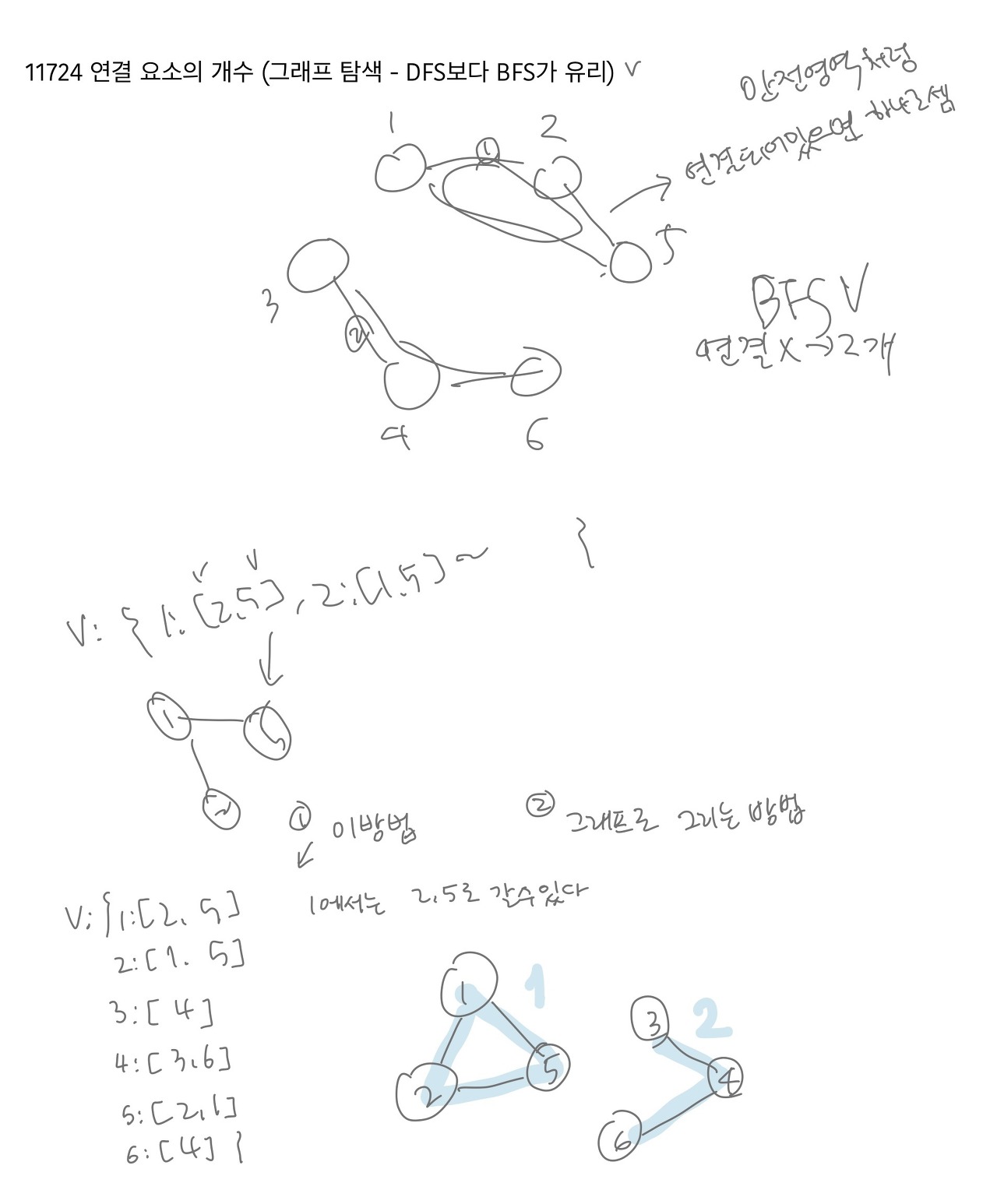
ㄴ 코드
import sys
input = sys.stdin.readline
N, M = map(int, input().split())
V = {}
for i in range(1, N + 1) :
V[i] = [] # 빈 리스트 채워줌 V: {1: [], 2: [], ...}
for i in range(M) :
v1, v2 = map(int, input().split()) # 입력받는 행, 렬 1 2 일때 v1:1, v2:2
V[v1].append(v2) # V의 ┌ v1(1)번째자리에 v2(2)가 들어감
V[v2].append(v1) # V: {1: [2], 2: [1], 3:[]...} => 1번 노드는 2번 노드랑 연결되어있고..
# 반대로 넣는 이유? 어느 노드랑 서로 연결되어있는지 체크하려고
# print(V)
gone = [] # BFS가 실행될 때 gone을 다시 비워줌.
count = 0
def BFS(now) :
que = [now] # 큐를 만들고 큐에 나우 하나만 넣음
while que : # 큐라는 리스트에 아직 안 간 곳이 추가 됨
q = que[0]
gone.append(q) #방문했다고 체크 // 해당 노드 경로 봤으니 봤다고 넣어주고
del que[0] #체크했으니 지움
for i in V[q] : # V: {1: [2,5], 2: [1,5], 3:[4], 4:[3,6],..}
if not i in gone and not i in que : # 이미 간 곳도 아니고 갈 예정도 아닐 때
que.append(i) # que:[] -> que: [2,3,4]
#que에 넣어서 i랑 연결된 노드들도 확인하게 함
for i in range(1, N + 1) :
if not i in gone : # 간 곳 중에 하나가 아니면
count = count + 1 # 연결된 별개가 하나 더 있는거니까 셈
BFS(i) # 정점의 갯수 n만큼 BFS 반복
print(count).
.
2606 바이러스
요건 앞에 푼 문제(11724 연결된 요소의 개수) 코드에서
BFS(1) 만 실행해서 count하면 되는 문제였다!
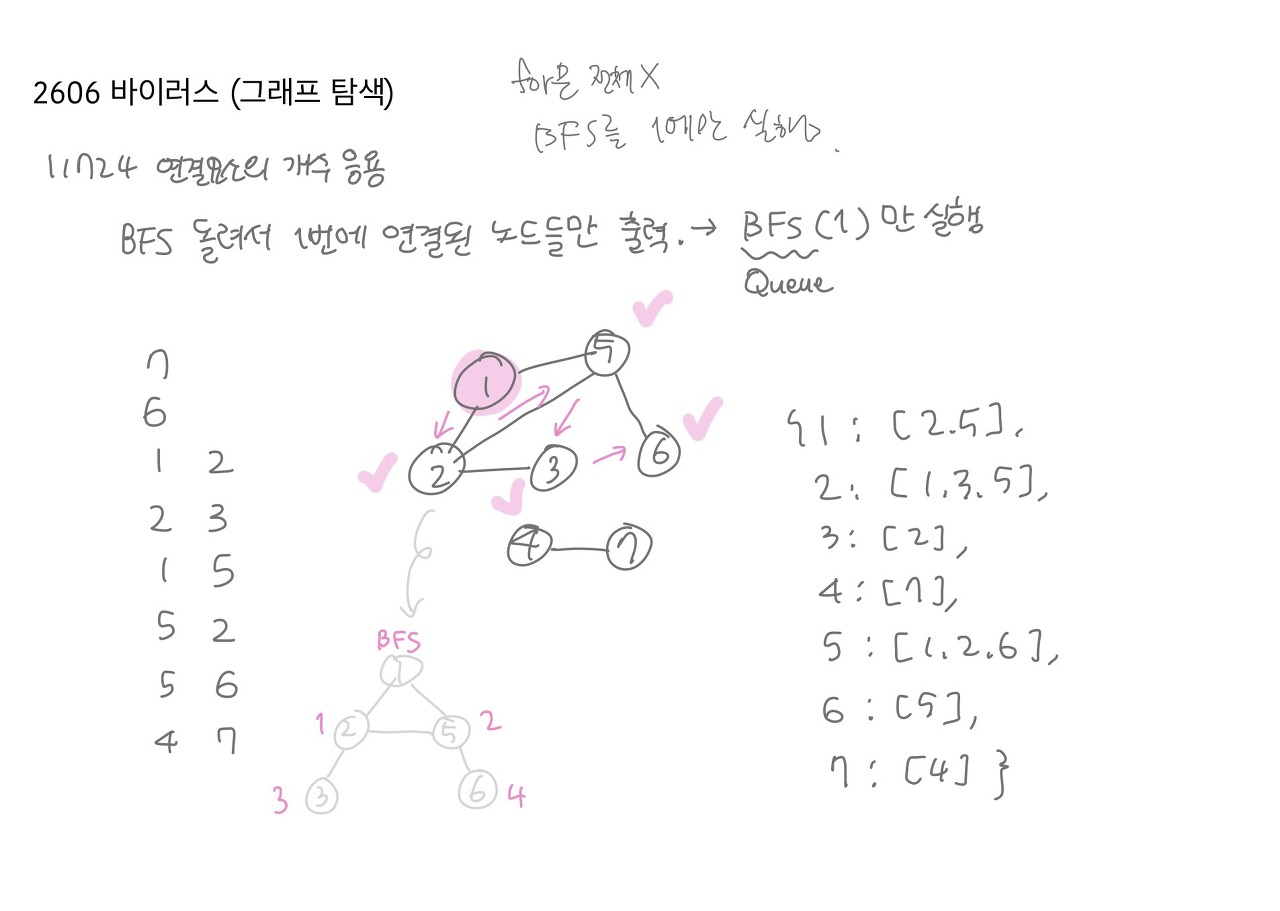
ㄴ 코드
import sys
input = sys.stdin.readline
# 정점 갯수, 간선 갯수, 탐색 시작할 정점 번호
Vn, En, v = map(int, input().split())
V = {} # {}: 딕셔너리. 간선이 연결하는 두 정점의 번호가 들어옴(입력값 V[v1], V[v2])
for i in range(1, Vn + 1) :
V[i] = [] # 빈 리스트 채워줌 {1: [], 2: [], ...}
for i in range(En) :
v1, v2 = map(int, input().split())
V[v1].append(v2)
V[v2].append(v1)
for i in range(1, Vn + 1) :
V[i].sort()
gone = []
def DFS(now) :
print(now, end = ' ') # 가장 먼저 자기를 출력
gone.append(now) # 그리고나서 자기가 갔던 곳에 넣음
for i in V[now] : # 나우를 갈 수 있는 i에 대해서 i가 아직 안 간 곳이라면 DFS를 실행
if not i in gone :
DFS(i) # 1에서 실행하면 1이 출력되고, 2에서 DFS가 시작돼서 2가 출력되고 4에 대해 DFS가 출력되고 끝남.
DFS(v) # 그리고 1에서 3도 갈 수 있으니 3에 대해 DFS가 출력됨.
print()
gone = [] # BFS가 실행될 때 gone을 다시 비워줌.
def BFS(now) :
que = [now] # 큐를 만들고 큐에 나우 하나만 넣음
while que : # 큐라는 리스트에 아직 안 간 곳이 추가 됨
q = que[0]
print(q, end = ' ')
gone.append(q)
del que[0]
for i in V[q] : # V: {1: [2,3,4], 2: [1,4], 3:[1,4], 4:[1,2,3]}
if not i in gone and not i in que : # 이미 간 곳도 아니고 갈 예정도 아닐 때
que.append(i) # que:[] -> que: [2,3,4]
BFS(v)2021.11.20 (토)
오늘의 이야기
주말이라고 쪼금 여유롭게 했던 것 같다....
정신차리구 일요일은 다시 빡세게 해야쥐
룰루랄라
요즘 근황은! 살짝 피곤하지만 하고싶던 공부를 하고 있어서 너무 즐겁다ㅎㅎ
열심히 '잘' 해야지
홧팅
'SW Jungle [예림] > Algorithm' 카테고리의 다른 글
| [WEEK03] DAY22 & TMI (0) | 2022.10.14 |
|---|---|
| [WEEK03] DAY21 & TMI (0) | 2022.10.14 |
| [WEEK03] DAY19 (0) | 2022.10.14 |
| [WEEK02] DAY18 & TMI (0) | 2022.10.10 |
| [WEEK02] DAY17 & TMI (0) | 2022.10.10 |




댓글